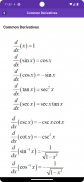
Calculus Formulas

Calculul este implicat în studiul „schimbării continue” și aplicării lor la rezolvarea ecuațiilor. Are două ramuri majore:

1:

Calcul diferențial

care se referă la ratele de modificare și pantele curbelor.

2:

Calcul Integral

privind acumularea de cantități și zonele de sub și între curbe.

Atât Calculul diferențial, cât și Calculul Integral folosesc noțiunile fundamentale de convergență a secvențelor infinite și a seriei infinite la o limită bine definită. Aceste două ramuri sunt legate între ele prin teorema fundamentală a calculului

Calculul diferențial împarte o zonă în părți mici pentru a calcula rata de modificare. În timp ce calculul Integral se alătură părților mici pentru a calcula aria sau volumul. Pe scurt, este metoda raționării sau calculului.

În această aplicație puteți vedea o listă de formule de calcul, cum ar fi formula integrală, formula derivată, formula limitelor etc.

Limitele Formulele conțin:

Definiții de limite.

Relația dintre limitele limită și cele unilaterale.

Formule Limită proprietăți.

Formule de evaluare a limitelor de bază.

Formule tehnici de evaluare.

Unele funcții continue.

Teorema valorii intermediare.

Rezolvați orice limită de calcul.

Formulele derivate conțin:

Definiție și notare derivate.

Interpretarea derivatului.

Proprietăți și formule de bază.

Derivate comune.

Variante de regulă în lanț.

Derivate de ordin superior.

Diferențiere implicită.

Creștere / Scădere - Concavă sus / Concavă în jos.

Extrema.

Teorema valorii medii

Metoda lui Newton.

Ratele aferente.

Optimizare.

Formulele integrale conțin:

Integrații Definiții.

Teorema fundamentală a calculului.

Proprietăți.

Integrale comune.

Tehnici de integrare standard.

Integral impropriu.

Aproximativ Integrale Definite.

Aplicație foarte la îndemână pentru studenții de matematică.